POINT ELASTICITY FOR QUADRATIC DEMAND FUNCTION
The quadratic demand function is
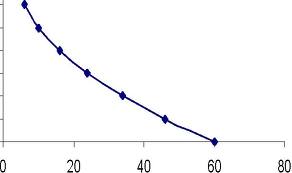
Qd = 60 – 15P + P2
Assume different values of price e-g from 0 to 10. Put these values in this equation and find out the quantity demand. Here we take price from 0 to 3.
|
P |
60 |
-15P |
P2 |
QD:60-15P+P2 |
|
0 |
60 |
0 |
0 |
60 |
|
1 |
60 |
-15 |
1 |
46 |
|
2 |
60 |
-30 |
4 |
34 |
|
3 |
60 |
-45 |
9 |
34 |
Then draw a figure, plot prices on vertical axis and quantity on horizontal axis. The resulting curve will be downward sloping curve.
To find the point elasticity of demand from this quadratic equation, differentiate it with respect to price,
Qd = 60 – 15P + P2
dQ/dP = -15 + 2P
IF P=3 then
dQ/dP = -15 + 2(3)
= -15 + 6
= -9
And
Qd = 60- 15(3) + (3)2
= 24
The formula of elasticity = (dQ / dP) (P/Q)
= -9 (3/24)
= -1.125
Its absolute value (ignoring minus sign) is greater than one so it is point elastic. Virtual University
